Hi everyone!! =) How was the test today? Do you all have fun answering all the questions? I hope you do. The test was a blast! Wasn't it??? LOL. =D. Anyways, we are at the end of chapter 3. I think I will miss learning rational functions, drawing graph I've never drawn before, looking for horizontal and vertical asymptotes, special case; hole in a graph???~ YEAH!! I will miss learning all that, don't you?? LOL...BYE, BYE chapter 3 hello chapter 4!
Advanced Function 12
Tuesday, 20 September 2011
Friday, 16 September 2011
Hi World of Blog!!!
Making a blog is something I've never imagine in my whole life....^__^. Thanks to this assignment I get the chance to do something that is beyond my expectation. During my school holidays about two months ago, i was very busy reading my friends' blog, very busy!!! =) Their blogs are very interesting and most of the story they posted teach me many lessons especially in life, which i have a lot to learn about. So, many people will think i will be influenced by my friends to create a blog of my own too. but unfortunately, they didn't manage to influenced me at all even there are some of my friends were. After the first day of school here in CPU, especially after Advanced Function class, i was so thrill to start doing the assignment. I was assign to create a blog of my own not about life but instead about ADVANCED FUNCTION....I was just like, whattttt??? It is possible??? at the same time thrill as well as i never thought of making a blog my whole life. Plus i do not know how. Even for this blog, i have my friend to help me. Credit to Siti Khadijah binti Muhammad Ariff for helping me, she's my housemate =). With her help, here i am writing my own blog as part of my homework.
Speaking of Advanced Function, this subject is quiet interesting. During high school, i only know two function: linear and quadratic. Now after attending Advanced Function class for almost two month, i found out that there are more two function. In fact there are more then two type of function and from those type of function there are more branches of function we can see. For this subject we will learn about the characteristics of each function, how to solve them, how to find the solution if they are inequality etc. Apart from that,
This is my first draft when I first started making this blog. See, i did not manage to finish it.....But now I am getting use to it. See the differences before and after.
This is my first draft when I first started making this blog. See, i did not manage to finish it.....But now I am getting use to it. See the differences before and after.
Making Connection With Rational Function and Equation.
OH mY GOD!!!! tHE Due date is today!! I haven't post the last sub chapter yet. Relax, take a deep breath.....PANIC!!! Ms. Joanne and Ms. Malar, please forgive me.....
This chapter is quite short. We can see an example of everyday life related to rational function. An example from the text book is, "Most of us know that getting closer in a concert means a better view, but it is also means more exposure to potential damage sound levels. The intensity, I, increase by what is known as the inverse square law, or reciprocal of the square of the distance, d, from the sound source, so that I=k/d^2. This law also applies to gravitational force and light intensity.", text book page 186.
The question:
The intensity of sound, in watts per square metre, varies inversely as the square of the distance, in metres, from the source of the sound. The intensity of the sound from the loudspeaker at the distance of 2 m is 0.001W/m^2.
a) Detemine a function to represent this relationship.
b) Graph this function.
c) What is the effect of halving the distance from the source of the sound.
__________________________________________________________________________________
The solutions:
a) So, I=k/d^2, k is constant.
substitute I=0.001 and d=2 into the equation to find k.
I=k/d^2
0.001=k/(2)^2
0.001=k/4
k=0.001 x 4
k=0.004
So, I=0.004/d^2
b) The graph:
The graph will looks like this, but the scale is different according to the equations. The y-axis represent the Intensity and the x-axis represent the distance. The equation of the graph should be written on the graph: I=0.004/d^2.
c) substitute 1/2d for d.
I= 0.004/(1/2)d^2
I= 0.004/(d^2/4)
I=4 x 0.004/d^2
Therefore if the distance is halved, the sound is four times as intense. In other word, the further you get to the stage of the concert the high the exposure to potentially damaging sound levels.
I have finish the question!!!Hope you all understand. I also hope you all can answer a similar question as this one, as most of the question is using the same method.
oNE, Last thing, the special case:
The special case is that there is discontinuous at a point where if we calculated manually we will say that it is the restriction and the vertical asymptote. But if we graph the function using the gc, we will see there is no discontinuous in the graph. If we want to identify which point is the discontinuous point we just have to substitute the value then see the result. If the the result does not approaches negative or positive infinity instead the results is a whole number, thus that value is the point where the discontinuous is. In other word, we can just say there is a hole at the point (x,y). This is an example of a graph with a hole.
That is all for chapter 3.5 and unfortunate it is the end for this chapter. Later I will see you all again in with chapter 7 ahead. I am looking forward to the next chapter that i will post in a few months time. Bye!!!
Thursday, 15 September 2011
Solving rational equation and inequalities.
Hi, my beloved friend. Seriously now, I am really not in the mood of writing. So just enjoy this video. For real.
All this video cover the whole chapter 3.4. I think, there's no need to explain in words anymore. Plus I am really not in the mood of writing. So I hope you enjoy this video. I just want to say that there are 3 method we can use to solve rational equation and inequalities.
1. Using normal method to solve algebra expression, but this is only for rational equation not inequalities.
2. Using number line and test value.
3. Using the graph, we have to draw the graph and observe the solution in the graph.
Thumbs up everybody!! We are at the end of this chapter. And I can assure that learning this chapter is more interesting with the three video above. Have fun reading my it!! See you next time, Bye!!!
Rational Function
Hi there!!! We meet again. I am not in the mood to write something. So just enjoy this video about rational function.
Upps... sorry I cannot find any video that are related to our syllabus, this is because rational functions is so wide thus the video i found talks about reciprocal, not what we learn in this chapter. But this video up there is a portion of what we learn in class. So I have no choice and just have to write it.
The general equation for rational functions is f(x)=ax+b/cx+d {a,b,c and d E R}.So i will demonstrate to you the key features of the function using the a,b,c and d term.
The general equation for rational functions is f(x)=ax+b/cx+d {a,b,c and d E R}.So i will demonstrate to you the key features of the function using the a,b,c and d term.
- Domain - {x E R, x cannot equal to -d/c}
- Range - { y E R, y cannot equal to a/c}
- x-intercept - x equal to -b/a.
- y-intercept - y equal to b/d.
- vertical asymptote - x equal to -d/c.
- horizontal aymptote - y equal to a/c.
- restriction - x cannot equal to -d/c.
How to find horizontal and vertical asymptotes manually?
1. Horizontal asymptote
- We have to substitute x negative infinity and positive infinity into the equation.
- and see the y values approaches what value, that value is the horizontal asymptote.
- or even easier just divide all the term in the equation with the x term with the highest degree
- To find the vertical asymptote we have to substitute the closest value of the restriction from the left and from the right.
- The result must approaches negative and positive infinity. If not the restriction is not the horizontal asymptote.
HUH!!! Is that how to find the vertical and horizontal asymptote?? YES!! That's the way. In case if there are a question about how to find the VA and HA and required to show the solution, just use the method above. I think that all for now. See you next time!! bye!!
Reciprocals of a Quadratic Function.
HA....(yawning). Look at the time it is 5.00 in the morning!! Last night I was preparing for my presentation for International Business, then I thought of writing my blog after that. Unfortunately, I was so sleepy. I took my pillow and sleep on the floor, hoping that I will woke up at_____maybe_____around three a.m. However, I did not manage to do so even though I slept on the floor. And now, here I am telling you all my sad story........
Anyways, let's get to the real stuff. Today, we are still in chapter 3, so previous post we learn about the reciprocal of a linear. We discover how its looks like and also we describe the key features of the function. For today's lessons we will doing the same thing, but using quadratic function.
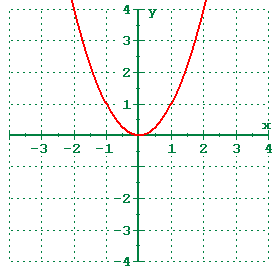
How does quadratic function looks like? Basically quadratic function has this form of general equation, (F(x)=ax^2+bx+c). For example, f(x)=5x^2+10x+1. The shape of the graph is like this :
Anyways, let's get to the real stuff. Today, we are still in chapter 3, so previous post we learn about the reciprocal of a linear. We discover how its looks like and also we describe the key features of the function. For today's lessons we will doing the same thing, but using quadratic function.
How does quadratic function looks like? Basically quadratic function has this form of general equation, (F(x)=ax^2+bx+c). For example, f(x)=5x^2+10x+1. The shape of the graph is like this :
This graph may not shown the actual measurement for the example of equation I gave you, but this how quadratic function looks like. Now lets see how the reciprocal of quadratic looks like...
Again, this picture may not show the real exact measurement of the equation given but still this is how reciprocal of quadratic looks like. Now lets discover and describe the key feature of this reciprocal ;
- The restriction on the domain - the denominator cannot be zero, so equate the denominator to zero and calculate the x-value.
- Domain and range - { x E R, x cannot equal to the restriction}, { y E R, y cannot equal to the horizontal asymptote}
- x-intercept and y-intercept - To find the x-intercept we have to substitute y=0, y-intercept we have to substitute x=0.
- The end behaviour
- as x approaches vertical asymptote from the left, y approaches......and as x approaches vertical asymptote from the right, y approaches.........
- as x approaches negative infinity, y approaches........and as x approaches positive infinity, y approaches........
- The horizontal asymptote is equal to the restriction of domain, the vertical asymptote equal to the restriction of range.
- We can also use the increasing and decreasing interval or the increasing and decreasing of slope to describe the key features of a reciprocal of quadratic.
Here are videos about reciprocal of quadratic function in details.
These three videos explain in details about reciprocal of a quadratic function. It shows how to find the key features of reciprocal and also how to draw the graph without using graphic calculator. Enjoy!! See you next time with chapter 3.3....Bye!!
Sunday, 11 September 2011
Reciprocal Of Linear
Hi everyone!!! Just like i promise, we meet again. For this time, i will continue with chapter 3. Basically this chapter is about the reciprocal of each function. We will learn the characteristics of each reciprocal. For this 3.1 sub-unit we will learn the reciprocal of linear.......Let's get started!
Before getting to know the reciprocal of linear lets identified a linear function first. A linear function is a function with a highest degree of one. Let me give you an example of an equation of a linear; f(x)=2x-3 or maybe more simple, f(x)=x. The graph is like this:
Sorry, i cannot find a graph with scale on it. But this is how f(x)=x graph's looks like. So the reciprocal of this f(x)=x is just f(x)=1/x. The numerators must be a constant but not necessarily one, any number can be and the denominator is the linear function. Lets take a look how a reciprocal of f(x)=x looks like;
Wow!! Graph with scale and more amazing drawn on a graph paper.....So, this is how a reciprocal of linear looks like. Okay now it is time to identify the characteristic of the graph.
- The restriction on the domain - the denominator cannot equal to zero, so x cannot equal to zero.
- The asymptotes - x=0 is the vertical asymptote, while y=0 is the horizontal asymptote.
- Domain and range - {x E R, x cannot equal to 0}, {y E R, y cannot equal to 0}
- The end behaviour -as x à 0 from the left, y à ∞, as x à 0 from the right, y à −∞, as x à∞ from the left, y à 0, as x à−∞ from the right, y à 0
- The intercept - reciprocal does not have intercept.
0=1/x
x=1/0
x=1/0 is undefined so there are no x-intercept.
y=1/0
y=1/0 is also undefined so there are no y-intercept as well.
- As the graph approaches the vertical asymptote the slope of the graph become steeper.
- As the graph approaches the horizontal aymptote the slope of the graph become less steeper.
- Increasing interval= the interval when x increased, y increased.
- Decreasing interval= the interval when x decrease, y decrease.
So that's all for this chapter. I already describe the characteristics of the reciprocal. Look forward to my next post, as i will continue with chapter 3.2!! Bye!!
Subscribe to:
Posts (Atom)